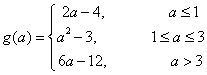高中数学中数形结合思想在函数解题中的运用

中山市实验高中   单尧

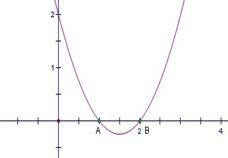
内容摘要：本文主要是研究数形结合思想在函数解题中的一些应用，对如何求函数的定义域、值域、单调性、奇偶性及其解析式等五个方面进行了简单分析。通过对几个典型例题的剖析，进而得出数形结合在函数解题方面的强大功用。

关键词：数形结合、函数

正文：

数学是研究客观世界的空间形式和数量关系的科学，数与形是数学的两种表达形式，数十形的抽象概括，形又是数的直观表现。数形结合并不是简单的堆砌，而是有机的结合。华罗庚教授曾说过：“数缺形时少直觉，形少数时难入微。数形结合百般好，隔裂分家万事非。”数形结合是把抽象的数学语言同直观的图形结合起来，通过“以形助数”、“以数解形”，使抽象思维和形象思维相结合，通过图形的描述、代数的论证来研究和解决数学问题。而对于抽象思维还不够成熟的高中学生来说，如果在解题中能够很好的运用这一数学解题中最重要的方法之一，就能够使复杂的问题简单化，抽象的问题具体化，进而简化解题过程，从而达到事半功倍的效果！

（一）数形结合在求函数定义域方面的应用

例1：求函数的定义域.

解析：若要解决该函数的定义域，

则有，要解决此类不等式的解集，

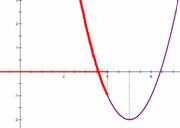
需要借助图像，如右图：

由图像可以看出，若要，

只需或，再由，得出该函数的定义域即为：.

小结：随着学生做题熟练程度的增强，二次不等式的求解已不用再画图。因此在求函数定义域方面，多见于画数轴选择出取值范围。

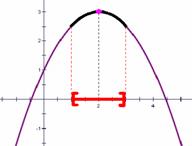
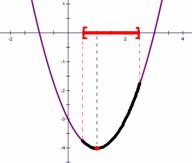
（二）数形结合在求函数值域方面的应用

例2：求函数的值域.

解析：看到所求函数为二次函数，由于函数

是非单调的，所以并不能代端点值去求出值域，

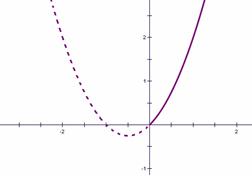
因此需要借助图像来观察，如右图：

借助图像的直观表达可知道，具有区间范围的

该二次函数的图像应为黄色区域部分，此函数的最

小值是在对称轴处取得，即当时，。

从而该函数的值域为：。

小结：对于此类问题是学生的常见出错点，学生们习惯于直接带入端点值得出其值域，因此对于给定区间上的二次函数值域问题，培养学生数形结合的思想是非常重要的。

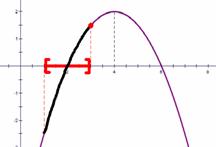
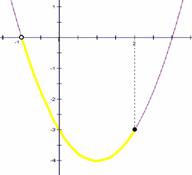
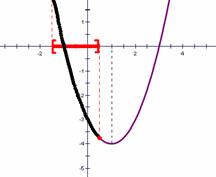
（三）数形结合在函数单调性方面的应用

例3：已知在上是减函数，求实数的取值范围。

解析：函数解析式中含有字母，因此函数在坐标系内的具体位置不能固定，需要画图分析，看何种情况才能满足题干要求：

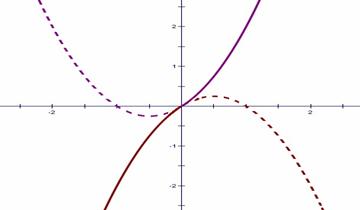
  通过图像分析可知：若要满足函数在给定区间上为单调函数，只能是后两种情况，也就是函数图像的对称轴不能出现在所给区间内，从而解题找到突破口。

  所给函数对称轴方程： ,由图像分析可知，需有，从而。

小结：该类问题常见于二次函数中，因其单调性与对称轴的位置有关，故通常画图分析更能直观得出题目所需情况，从而快速得出结论。

（四）数形结合在函数奇偶性方面的应用

例4：已知函数是定义在R上的奇函数，当时，.试求当时，函数的解析式。

解法一：若求时，函数的解析式，我们知道，从而满足题中所给条件，故有：，又由函数为上的奇函数，从而有，所以有。

解析：上作法是利用奇函数的定义，通过解析式来求得。

解法二：（1）画出函数在已知条件下的图像：当时，

（2）再利用函数是奇函数，从而函数图像关于原点对称，通过图像得出函数的解析式。

                                          

小结：通过对比两种解法，学生们更容易接受第二种。在对函数的理解上，高中学生还不能很透彻的明白，因此对引入数形结合的第二种解法学生更易接受，其直观、形象的优点更加突显出来。

（五）数形结合在函数求解析式方面的应用

   例5：（轴定区间变问题）已知函数，试求：在上函数的最小值.

解析：所给函数是已知的，但区间是可变动的，随着值的不同，区间位置发生变化，而对于二次函数这种非单调的函数来说，正如例2所说，其最值不能简单带入端点求解，故需画图帮助分析，如右图：

对称轴方程：。

(1) 当区间在对称轴左侧时，函数的最小值

是区间的右端点，即对应的函数值，也就是，

当,即时，函数的最小值是：

(2) 当对称轴处于区间内部时，函数的最小值

就是函数的最低点，也就是，当，即

时，函数的最小值是：

(3) 当区间在对称轴右侧时，函数的最小值

是区间的左端点，即对应的函数值，也就是，

当时，函数的最小值是：

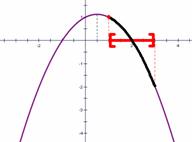
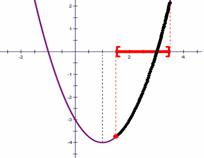
综上，函数的最小值 .

例6：（轴变区间定问题）试求函数在上的最大值。

解析：此类问题是所给区间已知，但所给函数位置不定，随着a 值的不同，函数在变。与上例相同，仍需画图分析：

函数可变为：，对称轴方程：。

（1）当对称轴在区间左侧时，函数的最大值

是区间的左端点，即1对应的函数值，也就是，

当时，函数的最大值是：

   

（2）当对称轴处于区间内部时，函数的最大值

就是函数的最高点，也就是，当时，

函数的最大值是：

(3) 当对称轴在区间右侧时，函数的最大值

是区间的右端点，即3对应的函数值，也就是，

当时，函数的最大值是：

综上，函数的最大值。

小结：此类型基本上是针对二次函数，有动有不动，解题时抓住不动，对动的因素考虑充分即可，主要还是考察对称轴与区间的位置关系。

以上只是借助几道例题简要说明了数形结合在解决函数问题方面的化繁为简的优点，但并不是说，理解了几个典型习题，就是领会了数形结合这一思想方法。学生要真正掌握数形结合思想的精髓，必须有雄厚的基础知识和熟练的基本技巧，所以要认真上好每一堂课，深入学习新教材的系统知识，掌握各种函数的图象特点，理解各种几何图形的性质。教师也要引导学生根据问题的具体情况，注意改变观察和理解问题的角度，揭示问题的本质联系，用“数”的准确澄清“形”的模糊，用“形”的直观启迪“数”的计算，从而使问题得到解决。在平日的教学中，教师要紧紧抓住数形转化的策略，沟通知识联系，激发学生学习兴趣，提高学生的思维能力。而且数形结合也不能只作为解题工具，只有充分揭示出数形结合的教育意义，深入挖掘其教育价值，数形结合在后续学习中才会有更旺盛的生命力，高中数学教学中数形结合提高解题能力的研究也才会有更宽、更好的奠基。只有这样，运用数形结合才能不断深化提高。

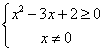
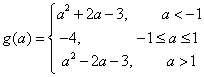                                               2009年10月30日